다이나믹 프로그래밍이란?
먼저 다이나믹 프로그래밍은 최단 경로를 구하는 다익스트라 알고리즘(Dijkstra algorithm)처럼 특정한 문제를 해결 할 수 있는 알고리즘이 아닌 문제를 해결하기 위한 접근 방식 중 하나이다. 즉 다이나믹 프로그래밍으로 풀 수 있는 문제들에 대해서 해당 문제를 푸는 것에 대해 생각의 틀을 제공해주는 프로그래밍 방법이다.
다이나믹 프로그래밍의 다양한 표현들
- 점화식
- 큰 문제를 작은 문제로 나누어 푸는 방법
- 과거에 구한 답을 활용하는 방법
- 메모이제이션
다이나믹 프로그래밍을 나타내는 다양한 표현들이 있지만 기본 개념은 다음과 같다.
- 재귀적으로 생각하기 + 불필요한 계산 줄이기(중복 제거하기)
재귀적으로 생각하기 ≒ 귀납적으로 생각하기
작은 문제는 해결이 되어 있다는 믿음을 가지고 큰 문제를 해결하는 방법이다.
피보나치 수열을 예를 들어보자. f₀ = 1, f₁ = 1, f𝑛 = f𝑛-₁ + f𝑛-₂(𝑛 ≥ 2)식에서 f의 n번째 수열을 구하려고 한다면 f𝑛-₁ 와 f𝑛-₂의 수가 계산이 되어 있다고 생각을 하고 두 수를 더해 f의 n번째 수열을 구한다.
여기서 f𝑛은 큰 문제, f𝑛-₁와 f𝑛-₂는 작은 문제로 볼 수 있다.
이 방법을 자바스크립트 코드로 옮기면 다음과 같다.
// 큰 문제
function f(n) {
if(n <= 1) return 1;
// f(n-1), f(n-2) 작은 문제
return f(n - 1) + f(n - 2);
}성능은 어떨까?
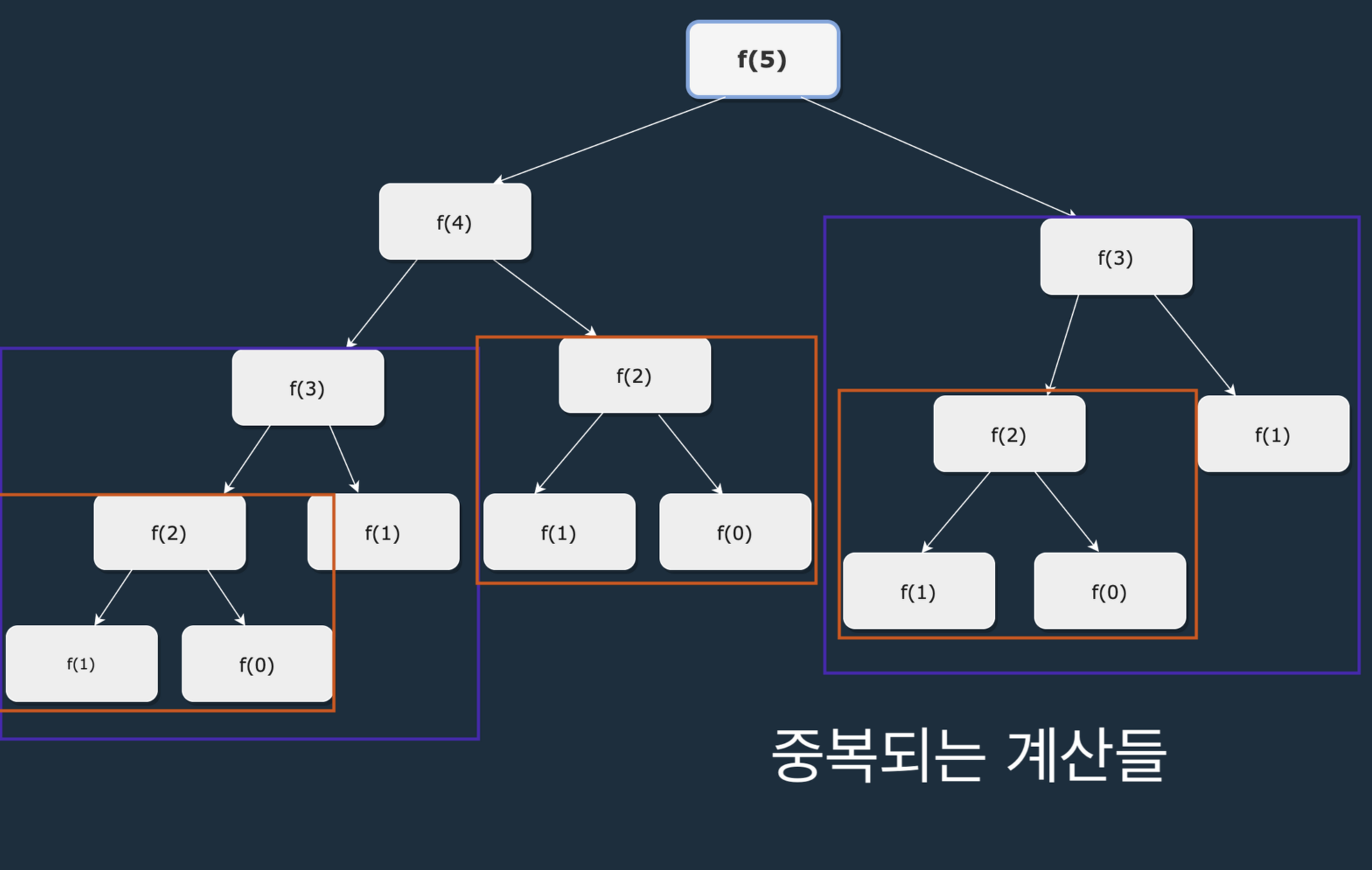
f(5)를 구하기 위해 f(4)와 f(3)을 호출, f(4)를 호출하기 위해 f(3), f(2)을 호출...이런 계산들이 수행이 되고 결국 중복되는 계산들로 인해 낭비가 발생하게 된다. 만약 그 수가 크다면 낭비는 더욱더 크다.
따라서 다이나믹 프로그래밍은 이런 재귀적인 사고방식에 불필요한 계산을 줄이는 기술을 더하는 것과 같다.
해결책1 : 메모이제이션
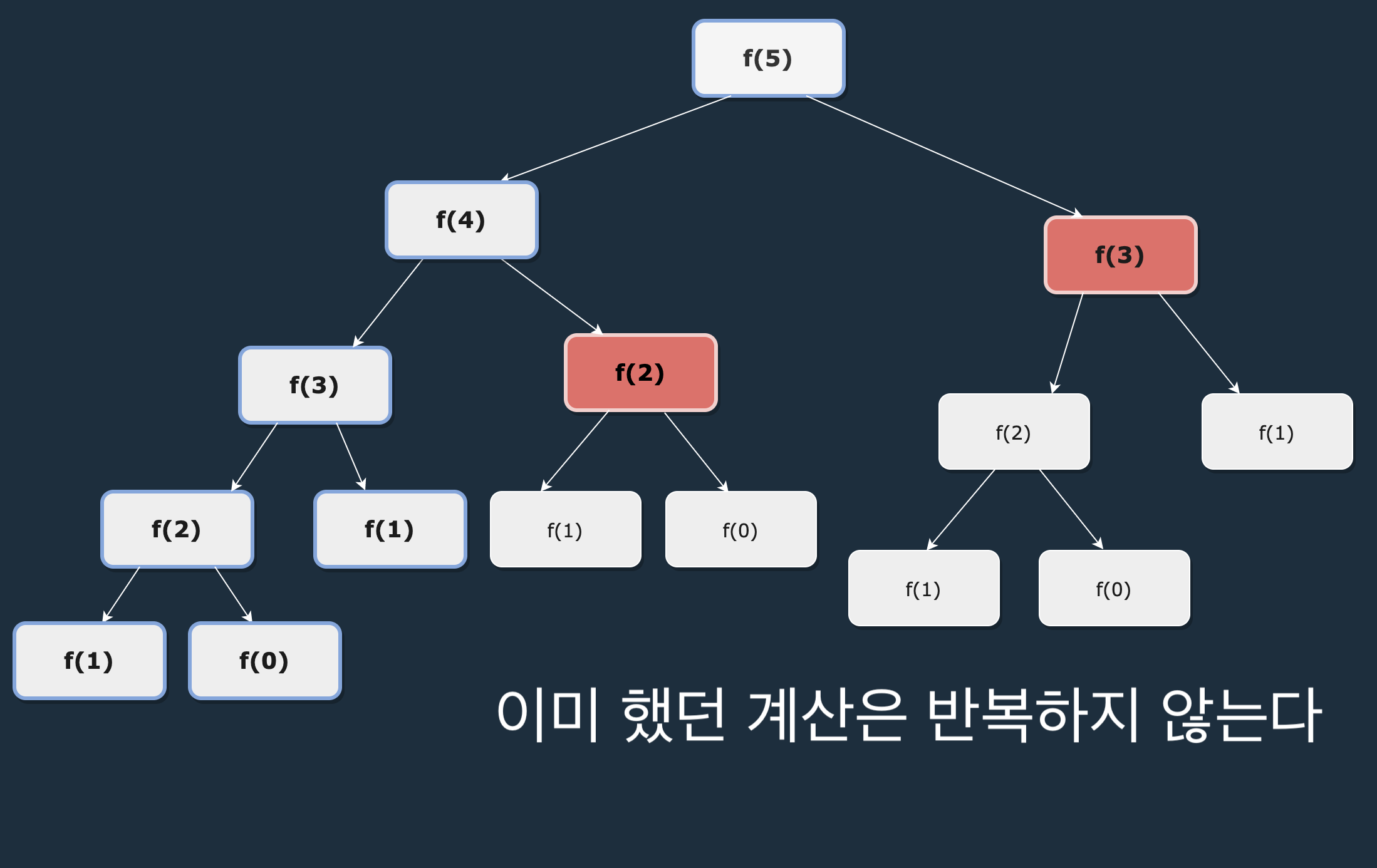
똑같은 코드를 수행했을 때 오른쪽의 f(4)의 계산을 보자. f(4)의 계산에서 이미 f(2)와 f(3)의 계산을 수행했기 때문에 저 값을 기억한 후 오른쪽의 f(2), f(3)을 계산할 필요 없이 기억한 값 그대로를 반환하면 밑의 불필요한 계산을 피할 수 있다.
이 방법을 코드로 나타내면 다음과 같다.
let memo = [];
function f(n) {
if(n <= 1) return 1;
// 이미 계산된 값이 있다면 그 값을 반환
if(memo[n]) return memo[n];
return memo[n] = f(n - 1) + f(n - 2);
}계산한 값들을 memo 배열에 저장을 하고 이미 계산한 값들은 바로 반환을 하는식으로 중복된 계산을 하지 않을 수 있다.
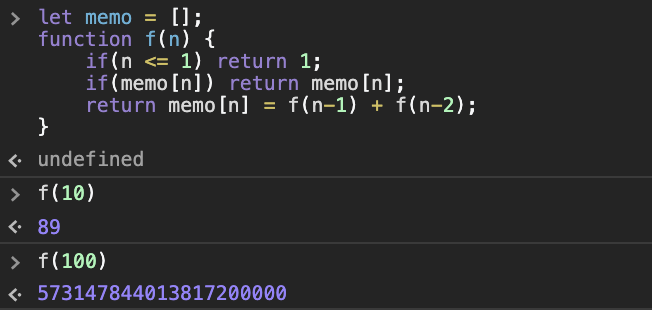
기존 코드로 f(100)을 호출 시 노트북이 굉장히 뜨거워지고 3분 이상 계산이 되지 않아 결국 브라우저를 종료했다. 하지만 메모이제이션을 사용했을 땐 무난하게 값이 나온다.
해결책2 : 밑에서부터 계산하기
또 다른 방식으로 불필요한 계산을 줄이는 방법은 밑에서부터 계산하기가 있다. 마찬가지로 피보나치 수열로 예를 들어보자.
f₀ = 1, f₁ = 1, f𝑛 = f𝑛-₁ + f𝑛-₂(𝑛 ≥ 2)식에서 보통 사람이 계산할 때는 밑에서부터 계산을 하는데,
이 방식을 똑같이 적용해서 배열에 f(0)에 1, f(1)에 1을 넣고 f(2)부터 계산을 해서 2, 3, 5, 8...이런식으로 한 번씩 계산을 해서 값을 얻어내는 방식이다.
| f(0) | f(1) | f(2) | f(3) | f(4) | f(5) |
| 1 | 1 | 2 | 3 | 5 | 8 |
이 방식을 코드로 옮기면 다음과 같다.
let f = [1, 1];
function calculateOnce(n) {
for(let i = 2; i < n; i++) f[i] = f[i-1] + f[i-2];
}반복문을 돌며 밑에서부터 계산을 해나가기 때문에 큰 수라 하더라도 계산한 값들이 배열에 저장되어 있어서 중복 계산을 하지 않는다.
이 방식 또한 f(100)을 무난하게 수행한다.
이 두 방법을 통틀어 다이나믹 프로그래밍이라고 부른다.
따라서 메모이제이션, 밑에서부터 계산하는 이 두 방법을 다이나믹 프로그래밍이라고 할 수 있다.
피라미드 형태의 지나간 수들의 최댓값 구하기
다이나믹 프로그래밍을 적용할 수 있는 예제를 하나 풀어보자.
피라미드 형태로 수들이 주어질 때, 꼭대기에서 아래로 내려오면서 지나간 수들의 합의 최댓값은 무엇일까?(단, 내려올 때는 반드시 자신의 바로 아래 두 수 중 한 군데로 내려가야 한다.)
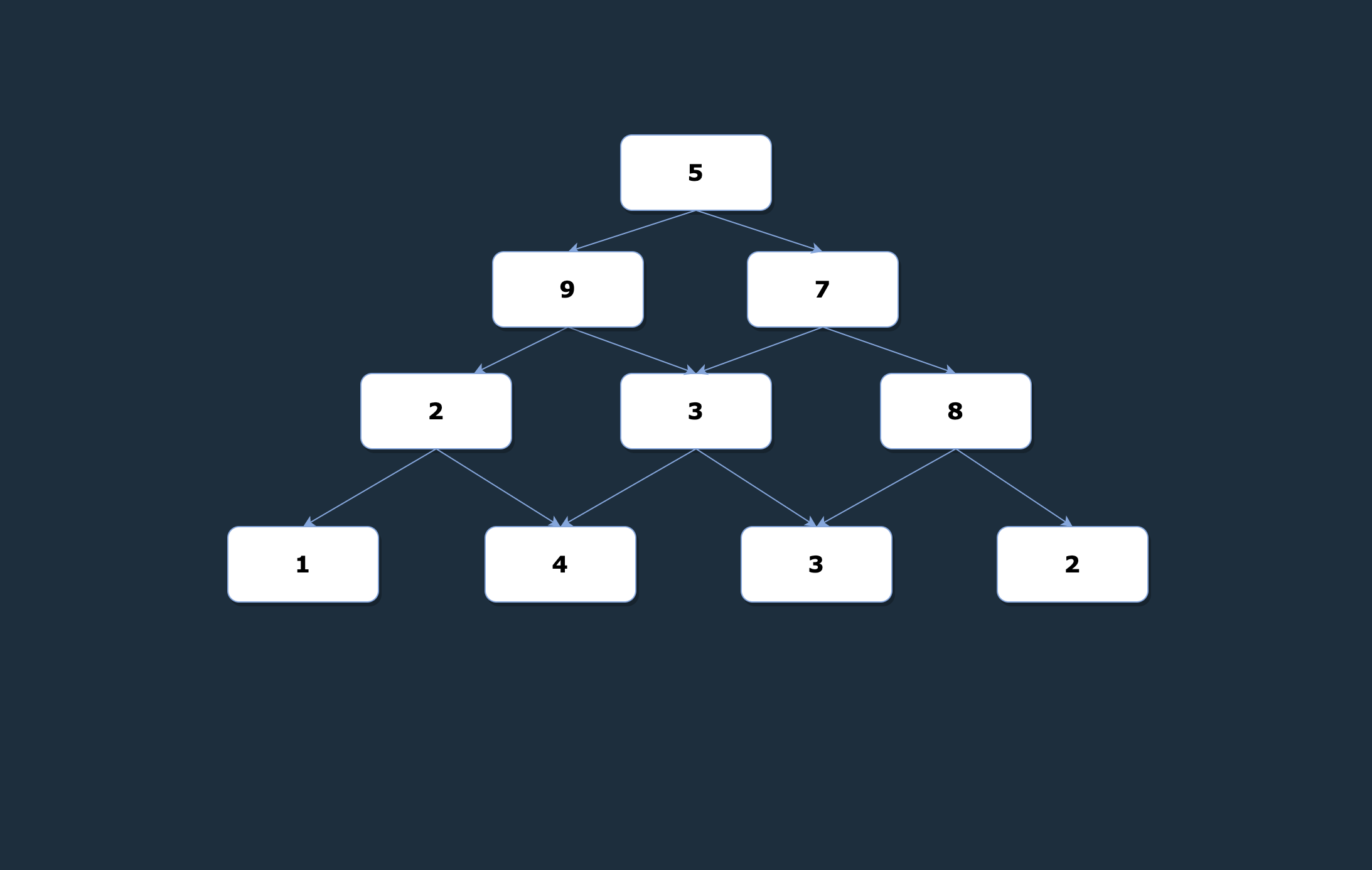
여기서 단순하게 (왼쪽, 왼쪽, 왼쪽), (왼쪽, 왼쪽, 오른쪽) ... (오른쪽, 오른쪽, 오른쪽)의 8가지 경우 중에서 최댓값을 구하면 되긴 하지만 좀 더 효율적인 방법으로 풀어보자.
재귀적인 사고 방식
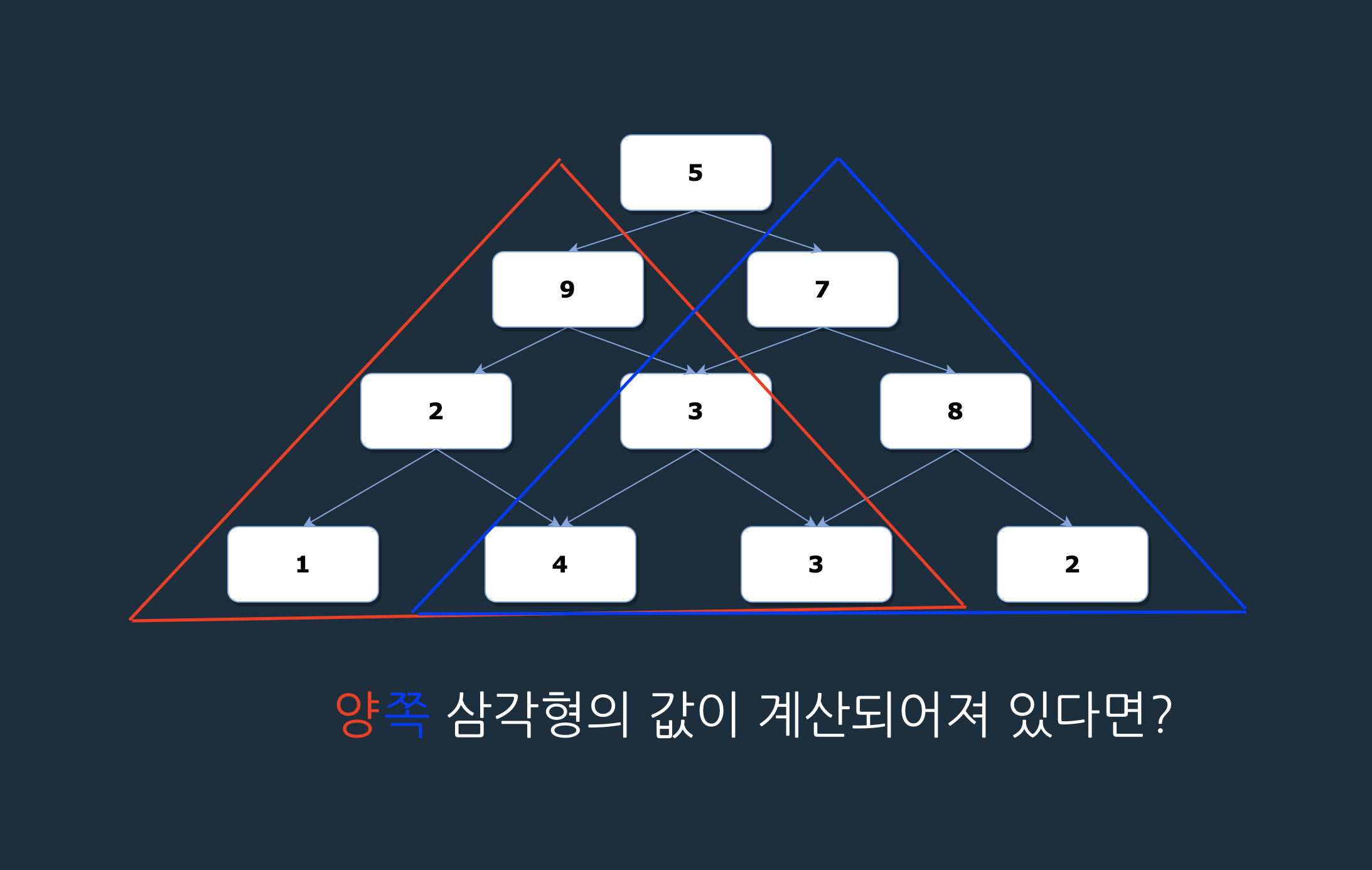
양쪽 삼각형의 값(작은 문제)이 계산되어져 있다고 생각을 하면 피라미드의 최댓값(큰 문제)은 다음과 같다.
- 꼭대기 숫자 5 + (둘 중 큰 값)
이런식으로 작은 문제들이 해결 되었다고 가정을 하면 전체 문제를 빠르게 해결할 수 있다.
따라서 f(x)를 현재 위치 x의 아래 삼각형만 봤을 때의 답을 정답이라 가정을 하고, 코드로 옮기면 다음과 같다.
function f(현재 위치) {
if(현재 위치가 바닥) return 현재 위치에 적힌 수;
return (현재 위치에 적힌 수)
+ Math.max(f(현재 위치의 왼쪽 아래), f(현재 위치의 오른쪽 아래));
}여기에 더불어 메모이제이션 또는 밑에서부터 계산하기를 적용하면 효율적인 해답을 구할 수 있다.
💡 유튜브 IOI KOREA 채널의 [알고리즘 강의] DP1. 다이나믹 프로그래밍이란 영상을 토대로 정리한 글입니다.
'Algorithm' 카테고리의 다른 글
| [백준] 단계별로 풀어보기 1단계 | Node.js (0) | 2021.06.24 |
|---|---|
| [프로그래머스] 가장 큰 정사각형 찾기 | JavaScript (0) | 2021.06.23 |
| [프로그래머스] 124 나라의 숫자 | JavaScript (0) | 2021.06.19 |
| [프로그래머스] 키패드 누르기 | 카카오 인턴 코딩 테스트 | JavaScript (2) | 2021.06.18 |
| [프로그래머스] 소수 만들기 | Summer/Winter 코딩 테스트 | JavaScript (0) | 2021.06.17 |
