문제 풀이
프로그래머스에서 알고리즘 문제를 풀다보면 수학적인 문제가 나올 때가 꽤 있는 것 같다. 이번 문제에선 대각선에 의해 잘라진 사각형의 개수를 구해서 풀 수 있었는데, 초등학교 5학년 경시대회 문제에서 답을 얻었다.
대각선과 만나는 격자점과 잘라진 사각형의 개수
대각선에 의해 잘라진 사각형의 개수는 격자점의 개수와 연관이 있다. 먼저 작은 수부터 차례대로 나열하여 규칙을 찾아보자.
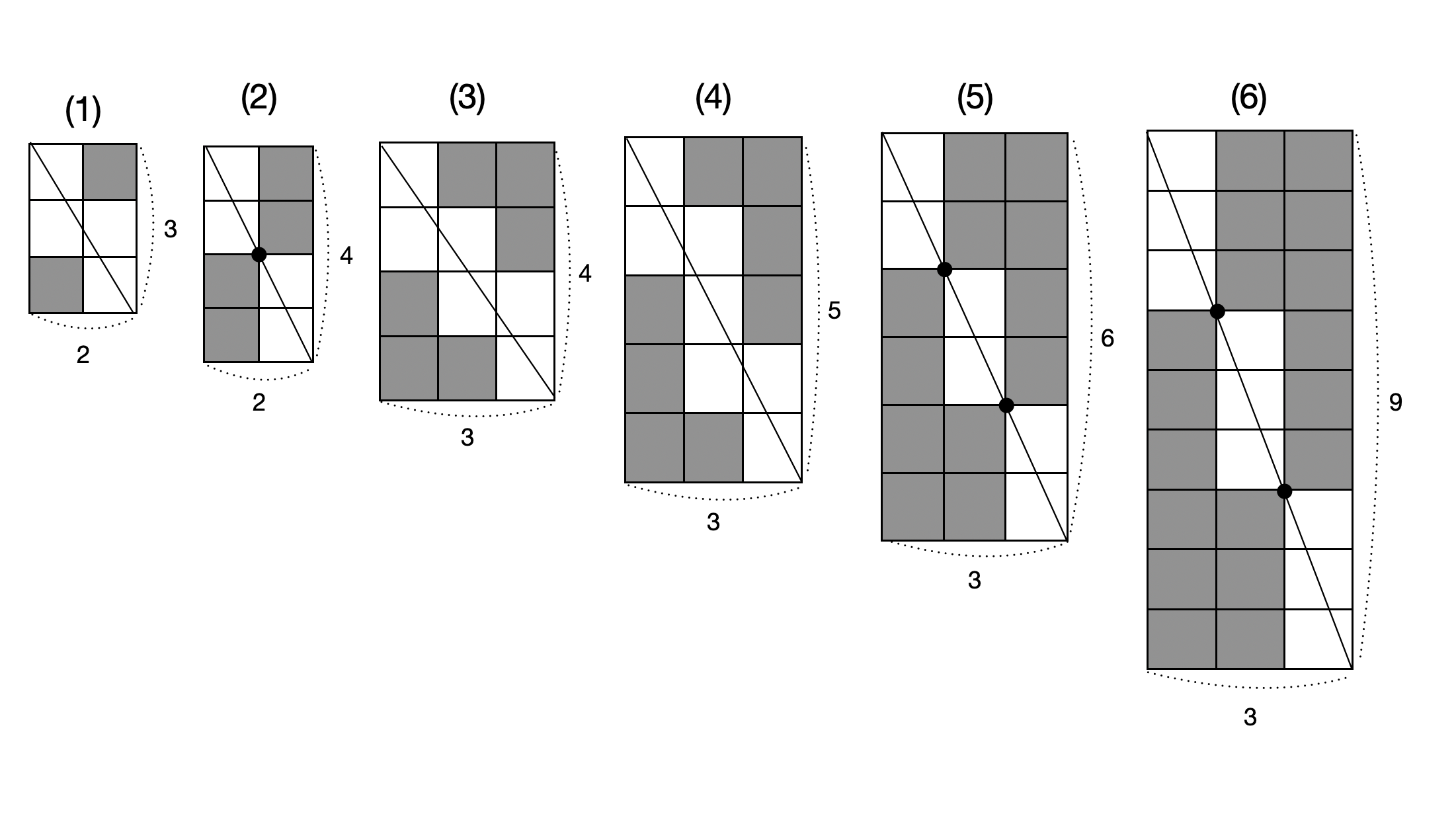
대각선과 만나는 격자점이 존재하는 (2), (5), (6)번 같은 경우 1보다 큰 가로와 세로의 최대공약수가 존재한다. (2)번의 최대공약수는 2, (5)번의 최대공약수는 3, (6)번의 최대공약수는 3이다.
여기서 규칙을 찾을 수 있는데 격자점이 존재하지 않는 (1)번, (3)번, (4)번은 '(가로) + (세로) -1'의 규칙으로, 격자점이 존재하는 (2)번, (5)번, (6)번은 '(가로) + (세로) - (가로와 세로의 최대공약수)'의 규칙으로 잘라진 사각형의 개수를 구할 수 있다. 따라서 문제에 나오는 길이가 8, 높이가 12인 경우 '8 + 12 - 4 = 16', 즉 잘라진 사각형의 개수는 16개이다.
이걸 바탕으로 코드로 옮기면 다음과 같다.
function solution(w, h) {
const answer = w * h;
const cut = w + h - gcd(w, h);
return answer - cut;
}
// 최대공약수 구하는 함수
function gcd(a, b) {
if (b === 0) return a;
return gcd(b, a % b);
}https://programmers.co.kr/learn/courses/30/lessons/62048?language=javascript
코딩테스트 연습 - 멀쩡한 사각형
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을
programmers.co.kr
관련글
[프로그래머스] 최대공약수와 최소공배수 | JavaScript
'Algorithm' 카테고리의 다른 글
| [프로그래머스] 신고 결과 받기 | JavaScript (0) | 2022.03.10 |
|---|---|
| [프로그래머스] 위장 | JavaScript (0) | 2021.08.17 |
| [백준] 단계별로 풀어보기 4단계 | Node.js (0) | 2021.07.09 |
| [프로그래머스] 올바른 괄호 | JavaScript (0) | 2021.07.02 |
| [프로그래머스] 땅따먹기 | JavaScript (4) | 2021.06.29 |
