피보나치 수
문제 설명
피보나치 수는 F(0) = 0, F(1) = 1일 때, 1 이상의 n에 대하여 F(n) = F(n-1) + F(n-2) 가 적용되는 수 입니다.
예를들어
- F(2) = F(0) + F(1) = 0 + 1 = 1
- F(3) = F(1) + F(2) = 1 + 1 = 2
- F(4) = F(2) + F(3) = 1 + 2 = 3
- F(5) = F(3) + F(4) = 2 + 3 = 5
와 같이 이어집니다.
2 이상의 n이 입력되었을 때, n번째 피보나치 수를 1234567으로 나눈 나머지를 리턴하는 함수, solution을 완성해 주세요.
제한사항
- n은 1이상, 100000이하인 자연수입니다.
입출력 예
| n | return |
| 3 | 2 |
| 5 | 5 |
입출력 예 설명
피보나치수는 0번째부터 0, 1, 1, 2, 3, 5, ... 와 같이 이어집니다.
코드
function getFibonacci(n) {
let fNum = [0, 1, 1];
for(let i = 3; i <= n; i++) {
fNum[i] = (fNum[i - 1] + fNum[i - 2])%1234567;
}
return fNum[n];
}
function solution(n) {
const answer = getFibonacci(n) % 1234567;
return answer;
}피보나치 수는 다이나믹 프로그래밍 글에서도 다뤘듯이 50번째 피보나치 수만 가더라도 그 수가 엄청나게 불어난다. 따라서 자바스크립트가 보장하는 정수계산을 넘어서게 되어서 제대로 된 값을 반환하지 못한다.
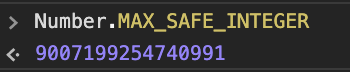

따라서 모듈러 연산의 성질을 이용해야 한다.
N으로 나눈 나머지를 반환하는 문제는 십중팔구 "int64도 버티지 못할만큼 숫자가 엄청 커지니까 적당히 나눠라"는 늬앙스입니다.중간에 모듈러 연산을 안해주면 일찍이 오버플로우가 발생했을테니 오답이죠.
- 프로그래머스 aerocode님
따라서 문제에서 1234567로 나누라는 의미는 "자, 이 문제는 int 자료형이 버티질 못해. 그래서 1234567로 나눠서 문제를 해결해봐!"라는 말이다. 그 문제 해결은 모듈러 연산의 (A + B) % C ≡ ( ( A % C ) + ( B % C) ) % C라는 성질을 이용한다. 계산 결과에 매번 1234567로 나눈 나머지를 반환하는 것으로 int 범위 내에 항상 값이 존재함을 보장할 수 있다.
참고
문제의 지문이 명백하게 잘못됬음에도 조치가 없는 이유는 무엇인가요? - 프로그래머스 질문글
반응형
'Algorithm' 카테고리의 다른 글
| [프로그래머스] 땅따먹기 | JavaScript (4) | 2021.06.29 |
|---|---|
| [프로그래머스] N개의 최소공배수 | JavaScript (0) | 2021.06.27 |
| [백준] 단계별로 풀어보기 3단계 | Node.js (0) | 2021.06.26 |
| [백준] 단계별로 풀어보기 2단계 | Node.js (0) | 2021.06.26 |
| [백준] 단계별로 풀어보기 1단계 | Node.js (0) | 2021.06.24 |
